ローンをすると利息が付きます。
不動産を購入するとき、殆どの方は住宅ローンで購入するかと思います。
また、事業を営んでいる方でも殆どの方は借金をします。
借金は悪いと思われる方も居るかと思いますが、実は事業を発展させる為に殆どの企業は借金をするのです。
借金をすることにより流動性資産を増やし、そのお金を投資に使って事業を拡大していくというのが一般的な会社です。
もちろん、借金しないで済むならその方が良いですが、中々できないものです。
このローンについては、利子が付きます。
利子の計算方法は色々あるので、ご自分で利息計算されたことのある方は少ないかもしれませんが、他人が計算して提示されたものが正しいかどうか確認したいと思いませんか?
住宅ローンなどでは、借入額も大きくなるので、計算に少しでも誤りがあると大きな金額になりかねません。
また、家を購入するときに実際に毎月どの位の金額を払えば良いか計算しくなるものです。
今回は、ローンに対する利息の計算方法や相続計算に使用する金利についてご説明します。

住宅ローン等の借金返済での確認事項
ローンの元金に対して幾らの利息が発生するかを計算する前に、先ず、幾つかのことを確認する必要があります。
- 単利なのか、複利なのか?
- 固定金利か、変動金利なのか?
- 毎月返済なのか、毎年返済なのか?
- ボーナス返済するのか、しないのか?
- 元利均等返済なのか、元金均等返済なのか?
- 返済回数で決めるのか、毎月の返済額で決めるのか?
- 利息分の端数を最初に精算するのか、最後に精算するのか?
以下で詳しく説明します。
用語の説明
利率に関わる主な用語は以下の通りです。
| 項目 | 内容 |
| 毎月の返済額 | 毎月の返済額です。 毎月の返済額が多すぎると、家計が圧迫され、返済が滞ることにもなりかねませんので、毎月の返済額は無理のない金額に設定しましょう。 |
| 総費用(総支払額) | 総費用(総支払額)とは住宅ローンを借りたことで発生する支払額の合計額です。 |
| 総費用(総支払額) | 住宅ローンを借りた場合には、毎月のローン返済以外に、以下の様な費用も掛かります。 金利や借入期間に応じた利息、借りる際の手数料、保証料、抵当権を設定する登記には登録免許税も必要です。 また、抵当権設定登記の手続きを司法書士に依頼する場合は司法書士報酬などもかかるため、こうした費用の合計額を総費用(総支払額)といいます。 総費用(総支払額)=毎月の返済額×返済回数+諸費用 ※ボーナス払いなし。金利が返済期間中変わらない場合。 |
| 月利 | 1ヶ月あたりの金利です。 金利とは、融資金額に対して支払う利息の割合のことです。 年利(実質年率)で記載されているケースが一般的なため、毎月の返済額を計算するときには「月利」に換算する必要があるため、12で割って月利を求めます。 |
| 返済回数 | 返済回数とは返済が発生する回数です。 毎月1回返済するのであれば、返済月数=返済回数となります。 なお、一般的には返済回数にボーナス払いの回数は含めません。 返済回数=借入年数×12 |
| 返済負担率 | 年収における返済額の割合です。 金融機関では、目安となる返済負担率を決めている場合があるため、目安を超える返済負担率に設定すると、シミュレーションの結果と審査結果が大きく乖離する可能性があります。 返済負担率を20%以下に設定すると、無理なく返済できる住宅ローンだと言われています。 |
| 借入額 | 住宅ローンで借りる金額の合計額のことです。 借入期間を長く設定すると、その分利息も増えてしまいますが、借入額と借入期間のバランスをとりながら、適切な金額を借りるようにしよう。 |
| 返済方式(2種類) | 住宅ローンの返済方式は、融資開始後、どのようにお金を返していくかを決めるものです。 住宅ローンの返済方式には、「元利均等返済」と「元金均等返済」の2種類があり、それぞれ特徴や計算式が異なります。 |
単利なのか、複利なのか?
単利とは、元金のみに金利をかけて利息額を計算する方法です。
一方、複利とは元金に一定期間ごとに発生する利息を加えたものを新たな元金とし、これに金利をかけて利息額を計算する方法です。
単利、複利の計算では、いずれも当初の元金は減らないことが前提となっています。
固定金利か、変動金利なのか?
金利については、契約時に金利が決まる固定金利と、借入期間中に適用される金利が変動する変動金利があります。
変動金利の場合には、毎月の返済額や総返済額を正確にシミュレーションできません。
また、変動金利の場合には、返済期間が変わる可能性もあります。
借入期間中に適用される金利(適用金利)が変動する金利タイプです。一般的に借入後は、半年に一度、適用金利の見直しが行われるものが多くなっています。
変動金利は、プライムレートとも言われ、「短期」と「長期」が存在し、物価上昇等の市場動向によって以下の様に決定されます。
| 短期プライムレート | 長期プライムレート | |
| 特徴 | 1年未満の短期貸出における最優遇金利 | 1年以上の融資を行う場合の最優遇金利 |
| 変動頻度 | あまり変動がない | 変動が激しい |
| 決め方 | 各銀行が金利を決めている | 債券市場に連動している |
変動の激しい長期プライムレートに対して、短期プライムレートはほとんど変動しません。基本的に、長期で貸し出すほうがリスクは高いので、一般的に、長期プライムレートのほうが短期プライムレートよりも金利が高くなります。

毎月返済なのか、毎年返済なのか?
借金は定期的に返済することを前提としているため、どの様な期間で返済するのかを決定する必要があります。
一般には、毎月返済か毎年返済となります。
なお、返済周期を決定するときは、返済日についても一緒に決定されます。
ボーナス返済するのか、しないのか?
借金の返済は、ボーナスを含めて返済を決める場合もあります。
通常ボーナス払いが発生するのは「毎月払い」としたときのみです。
ボーナス払いすることにより返済額が軽減される訳ではありませんが、通常は先払いとなるため実質的に総支払い額が減ります。
なお、通常、ボーナスの支払い周期は半年に1回にすることが多いですが1年に1回という場合もあります。
更に、ボーナス払いで返済する元金と毎月払いで返済する元金の割合も決定する必要があります。
例えば、5,000万円の元金を借金した場合に、毎月とボーナスの割合を5:5とした場合には、毎月返済分で2,500万円の元金返済、ボーナス分で,500万円の元金返済となります。
なお、返済表の表示上の問題ではありますが、ボーナス時の返済金額を毎月分+ボーナス分で表示する場合と毎月分とボーナス分を分けて表示する場合があります。
いくら借りられるのか迷ったときは、まずは自分の年収に返済負担率(20%程度)をかけて年間返済額を求めてみましょう。
(返済方式)元利均等返済なのか、元金均等返済なのか?
住宅ローンの利息額の計算では、毎月の返済によって元本が減ることを前提としており、返済後に残った元本に金利をかけて次回返済分の利息額を計算します。
このような利息額の計算方法を「残債方式」といいます。
このような前提があることから、先にご説明した「単利か複利か」という話はあまり意味が無い議論となってしまいます。
金利には「固定金利」と「変動金利」の2種類があります。
固定金利は、返済期間中の金利が一定です。
一方、変動金利は経済状況などによって金利が変動します。
一般的に、同時期で比較すると固定金利の方が変動金利よりも金利は高い傾向にあります。
住宅ローンに対する利息計算には、以下の2つの方法があります。
以下で詳しく説明します。
元利均等返済
元利均等返済とは、毎月の返済額が一定となる返済方法です。
元利均等返済の特徴は以下の通りです。
- 毎月の返済額が一定になるため、返済計画が立てやすい
- 返済額に占める元金・利息の割合が異なるので毎月の支払い額が一定となる
- 返済当初は利息分の支払いが多いので、借入残高が減りにくい
- 利息が増え、総返済額が元金均等返済よりも大きくなるので、返済期間が長くなる
住宅ローンは返済残高に対して利息がかかるため、基本的に返済初期は利息が多くなります。そのため、返済初期の高額な返済を避けるために有効な手段となります。
ただし、返済開始当初の返済額は、利息の占める割合が多いため元金が減るスピードが遅くなるので、支払い額が減っている実感がありません。
また、返済総額が多くなることが元利均等返済のデメリットといえます。
「元金+利息」の額が均等になるため、「元利」均等返済といいます。

元利均等返済の計算式
元利均等返済は月賦償還率(元利均等償還率)を借入額に掛けることにより求めます。
住宅ローンで初年度期首に借り入れた元本及び利息をn年後の完済までに均等額で返済するとき、いくらずつ返済すれば良いかを示す式です。
【元利均等返済】
毎月の返済額=借入額 X
r:月利(年利/12)
n:返済回数
※(1回目の利息は日割計算、2回目以降の利息は月割計算です)総返済額=毎月の返済額 × n
利息返済額=直前の借入残高 × r
元金返済額=毎月の返済額 - 利息返済額
元利均等返済の計算例
元利均等返済と元金均等返済の利息の計算方法とシミュレーションは次のとおりです。
〈計算条件〉
貸付額:6,000,000円 返済期間:5年 金利:2.0%
〈計算結果〉
毎月の返済額=105,166円
総返済額=6,309,060円
うち利息分 309,060円

元金均等返済
元金均等返済とは、返済額のうち元金の返済額が一定となる返済方式です。
ただし、毎月の利息部分の返済は変動する仕組みです。
元金均等返済の特徴は以下の通りです。
- 毎月の返済額に含まれる元金の金額が一定なので、返済が進むにつれて早く借入残高が減る
- 元利均等返済に比べて総返済額が小さいので返済期間が短い
- 利息が徐々に減り毎月の返済額も減っていくので支払いを実感しやすい
- 返済開始当初の返済額が最も大きくなるため、当初の返済負担が重くなる
元利均等返済と比べて契約当初の返済額が高額となる分、元金の返済スピードが速く、利息の総支払額を抑えることができます。
「元金」を均等に返済するので「元金」均等返済といいます。

元金均等返済の計算式
【元金均等返済】
毎月の返済額=借入額÷n+直前の借入残高 × rr:月利(年利/12)
n:返済回数総返済額=借入額+借入額×月利×(返済回数+1)×1/2
元金返済額=借入金額/(返済回数)
利息返済額=直前の借入残高×月利
元金均等返済の計算例
元金均等返済の利息の計算方法とシミュレーションは次のとおりです。
〈計算条件〉
貸付額:6,000,000円 返済期間:5年 金利:2.0%
〈計算結果〉
総返済額=6,305,000円
うち利息分 305,000円
元金返済額=100,000円

返済回数で決めるのか、毎月の返済額で決めるのか?
返済回数を指定した回数で支払うのか、それとも毎月の支払い額は同じとして支払い回数を決めるのかを決定します。
利息分の端数を最初に精算するのか、最後に精算するのか?
実際の支払い金額で発生する端数分(支払い金額と回数により発生する端数が出る回)を最初にするのか、最後にするのかを決めます。
住宅ローン返済を考える際の注意点
住宅ローンは、生活に無理が発生しないように決定する必要があります。
将来、家計に余裕がなくなり、ちょっとした臨時支出が住宅ローンの返済に影響を及ぼすこともあります。
また、何らかの事情で収入が減り、住宅ローン返済が厳しくなる可能性もあります。
住宅ローンは、途中で繰り上げ返済を実施すれば、返済期間や総返済額を減らすことも可能なので、最初は無理のない金額に設定しておく方が無難です。

銀行預金の金利と利息
金融機関でお金を預けると、金融機関から上乗せされる金額の割合を金利といいます。実際には、付いた利息から税金を差し引いた金額になります。
普通預金
普通預金の利息の計算方法は次の式です。
利息=期間中の毎日の最終残高の合計額 × 金利 ÷ 365
計算例
普通預金に100万円預け入れ(年利0.001%、入出金がない場合)
※税金は考慮しないものとします。
一日の利息は、100万円×0.001%÷365=0.0273…円となります。
一般的に普通預金の利息は年2回支払われるので0.0273…円を半年の182日で掛けると4.986…円になります。
その金額が半年ごとに支払われる利息金額です。
1円未満は切り捨てなので、1年後は、100万円+(4+4)=1,000,008円になります。
定期預金
定期預金の利息の計算方法は「単利」と「複利」があります。
「単利」と「複利」の違いについて説明します。
単利
単利は、当初預けた元金(金額)に対してのみ利息が付くものです。
単利=元金 × 金利
計算例
定期預金に100万円預け入れ(年利0.1%、預入期間3年の場合)
※税金は考慮しないものとします。
1年間の利息は100万円×0.1%=1,000円になります。
そして2年目以降も同じ元本100万円で計算をするので、2年目、3年目の利息も1,000円になり、3年間で3,000円の利息が付くことになります。
複利
複利は、一定期間ごとに発生する利息を当初預けた元本に組み入れて、利息を計算するものです。
複利=(元本 + 利息)×金利
計算例
定期預金に100万円預け入れ(年利0.1%、預入期間3年の場合)
※税金は考慮しないものとします。
1年複利の場合、1年目の1年間の利息は、単利の計算と同様で1,000円になり、2年目の元本は「元本100万円+利息1,000円で1,001,000円になります。
このため2年目の利息は1,001円になり、1年目の利息よりも増えます。
同様に3年目の元本は1,002,001円になり利息は1,002円になります。そうすると3年間で3,003円の利息が付くことになります。

財産評価のための利率計算
金利計算の方法
通常、税務計算で良く使用される金利の計算方法は以下の通りとなります。
なお、これらの、計算方法に対する計算式は、Excelにて関数でも提供されています。
| 利率 | 説明 | 計算式 | Excel関数 |
| 複利終価率 | 現在の元本がn年後の時点でいくらになるか、元金と利子の合計(元利合計)をするのが複利終価率です。 | 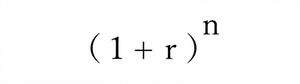 |
FV(r, n, 0, -1) |
| 複利現価率 | n年後の金額が現在ではいくらになるか、現在価値に割り引く計算に使うのが複利現価率です。 | 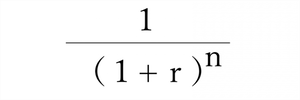 |
PV(r, n, 0, -1) |
| 年金終価率 | n年間一定金額を複利で積み立てたときの合計価額の合計金額を求める式です。 | 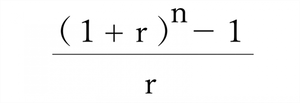 |
FV(r, n, -1, 0) |
| 償還基金率 | n年後の期末に一定金額を得るために、毎年期末に積み立てるべき金額を求める式 | 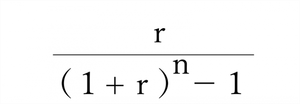 |
PMT(r, n, 0, -1) |
| 年金現価率 (複利年金現価率) |
n年間に一定金額を複利で積み立てたときの合計金額の現在価値を計算する式です。 複利年金現価率ともいいます。 |
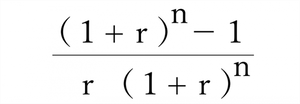 |
PV(r, n, -1, 0) |
| 年賦償還率 (元利均等償還率) |
年賦償還率は住宅ローンの返済額の計算によく使われる式です。 住宅ローンで初年度期首に借り入れた元金及び利息をn年後の完済までに均等額で返済するとき、いくらずつ返済すれば良いかを示す式です。 |
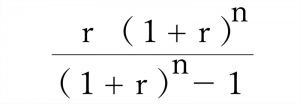 |
PMT(r, n, -1, 0) |
| r:利率 n:期間 ※年又は月 ※小数点以下3位未満四捨五入 |
|||

基準年利率とは
基準年利率とは、財産相続などの際にかかる相続税の割引率のようなもので、毎年その年によって違う数字が国税庁から発表されています。
財産評価額を割り引くための値ですが、最近は基準年利率が低く財産評価額が思ったより下がらないのが現状です。
その数字は近年においては年々大幅に引き下げられており、各方面の相続財産の評価額算出に大きく影響を与えています。
| 令和4年 | (単位:%) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 区分 | 年数又は期間 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
| 短期 | 1年 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| 2年 | |||||||||||||
| 中期 | 3年 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.05 | 0.05 | 0.05 |
| 4年 | |||||||||||||
| 5年 | |||||||||||||
| 6年 | |||||||||||||
| 長期 | 7年 以上 |
0.25 | 0.25 | 0.25 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.75 |
| 令和5年 | (単位:%) | ||||||||||||
| 区分 | 年数又は期間 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
| 短期 | 1年 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | |||
| 2年 | |||||||||||||
| 中期 | 3年 | 0.25 | 0.10 | 0.10 | 0.10 | 0.05 | 0.05 | 0.05 | 0.10 | 0.10 | |||
| 4年 | |||||||||||||
| 5年 | |||||||||||||
| 6年 | |||||||||||||
| 長期 | 7年 以上 |
1.00 | 1.00 | 0.75 | 0.75 | 0.50 | 0.75 | 0.50 | 0.75 | 0.75 | |||
(注) 課税時期の属する月の年数又は期間に応ずる基準年利率を用いることに留意する。
複利現価率とは
「複利」とは、利子にも利子がつくことですが、複利年金現価率は現金などを複利で一定期間運用していった場合、最終的な総額の現在価値を求めるための係数で以下の様な式で求めます。
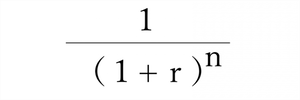
投資の世界などでは利益の計算にたまに使われる係数ですが、相続の計算ではたびたび登場します。
たとえば、もし被相続人(亡くなった人)が誰かに土地を貸していて、その期間があらかじめ決まっているような場合、相続税の計算には「複利年金現価率」が必要です。
複利年金現価率とは、現金などを積み立てて複利で一定期間運用していった場合の、最終的な総額の現在価値を求めるための係数です。
未来にもらえるお金を現在価値に当てはめるための値です。具体的には基準年利率で〇年間お金を運用して補償金と同額に戻るための比率です。
資金を定期的に積み立てて複利運用していった場合、将来実際に支払われるのは、支払い続けた積立金に、複利運用することで得られた利益をプラスしたものになります。
しかし、それはあくまで将来もらえる総額です。現在時点ではその総額どおりの価値はありません。また支払いを続けていくことで、その価値は変動します。
相続税の計算においては、定期借地権を評価する場合などに必要になります。なぜなら、相続時点における現在価値を求めてから相続税を計算する必要が出てくるためです。

定期借地権の評価額計算例
具体的に、相続の場面で複利年金現価率が必要となるのは、おもに定期借地権の評価額計算のときになります。
「定期借地権」とは期間の定めがある借地権(土地を借りる権利)のことです。
期限が過ぎると基本的には契約更新なしで土地を返却しなければならず、ほかの借地権に比べて、地主(土地の所有者)の権利が強くなっています。
ただし、定期借地権は基本的に相続の対象となります。
定期借地権の評価計算方法
定期借地権を相続した場合、相続税評価額は以下の算式によって計算されます。
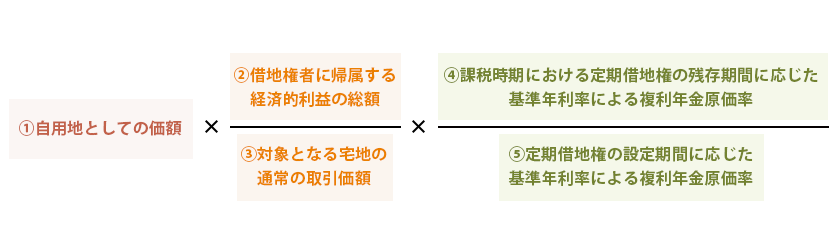
①自用地としての価額
②借地権者に帰属する経済的利益の総額
③対象となる宅地の通常の取引価額
④課税時期における定期借地権の残存期間に応じた基準年利率による複利年金現価率
⑤定期借地権の設定期間に応じた基準年利率による複利年金現価率
整理すると、【 ① × ②/③ × ④/⑤ 】ということになります。
定期借地権の評価額を計算するには、この①~⑤の値が必要になります。
①自用地としての価額
自用地の評価額は以下で求めます。
自用地評価額=路線価x地積[m2]
なお、自用地評価額の求め方は、以下の記事で詳細を説明しています。
②借地権者に帰属する経済的利益の総額
借地人が所有する経済的利益の総額を求めます。経済的利益とされるものは、例えば以下の通りです。
権利金などの額
権利金・協力金・礼金など借地契約終了時に返還をする必要がない金銭
保証金などの運用収益
保証金・敷金など借地契約終了時に返還をする必要がある金銭に関して、預託している間にその金額を運用したとした場合の利益
また土地の一般的な相場と実際に借地人が地主に支払う地代に差があるとき、取引事情や当事者間の関係性を総合的に考慮して、実質贈与だと認められる場合には、利益として差額の地代を含める必要があります。
③対象となる宅地の通常の取引価額
対象となる宅地の相場の評価額です。
実際に取引されている市場の評価額となりますが、もし分からない場合は、「定期借地権設定時の自用地の価額」 ÷ 0.8 とおき、計算することもできます。
路線価は毎年改定されますが、土地を貸した年の路線価を使います。
④課税時期における定期借地権の残存期間年数に応じた基準年利率による複利年金現価率
言葉だけを見ると非常にややこしいように思えますが、要は「いつ相続が発生したか」と「相続が起きた際に定期借地権があと何年残っているか」を基に、前述した基準年利率の表を確認し、さらにそこから複利年金現価率を導き出すということになります。
例えば、定期借地権の期間を50年と設定しており、10年経過した令和2年8月時点で相続が発生したら、課税時期は「令和2年8月」、残存期間年数は「40年」です。
これを対応する年度の基準年利率の表に当てはめると、
区分:長期
年数または期間:7年以上
となり、基準年利率は「0.1」、さらに対応する年度の複利表より残存期間40年の複利年金現価率は「39.191」となります。
⑤定期借地権の設定期間に応じた基準年利率による複利年金現価率
⑤の基となるのは④のように複雑な期間ではなく、もともと設定されていた定期借地権の契約期間となります。そのため、前述した例で言うと「50年」です。
この「50年」を基に対応する基準年利率の表に当てはめると④と同じく「0.1」、そして複利年金現価率は「48.747」となります。

まとめ
相続時には、財産額の評価をする必要があります。
借地には借地の評価方法、著作権には著作権の計算方法がそれぞれ決められています。
また、自宅を購入する場合には、住宅ローンをします。
それらの計算をするには、金利をどの様に求めれば良いかは、資金管理をする上で非常に重要です。
これらの計算に困った場合には、税理士に相談しましょう。
なお、以下の記事では、税理士の紹介をしていますので、是非ともご参照下さい。


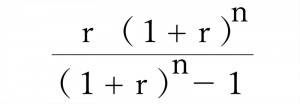

コメント